Матеріал 5-го класу.
1. Десятковий запис натуральних чисел.
Цифри запису числа розбиваються справа наліво на групи по три цифри, які називають класами.
Розклад числа на суму розрядних доданків:
2567 = 2 * 1000 + 5 * 100 + 6 * 10 + 7 * 1.
--------------------------------------------------------------------------
2. 1) Розв'язати рівняння - це означає знайти всі його корені або переконатися, що їх взагалі немає.
2) Корінь рівняння - це те число, яке при підстановці його замість букви, перетворює рівняння на правильну рівність.
--------------------------------------------------------------------------
3. 1) Основні поняття - точка і площина. Через дві точки можна провести тільки одну пряму. Пряма немає ні початку, ні кінця.
Промінь - це частина прямої, яка має початок.



Одиничний відрізок - це довжина відрізка, який обрали для вимірювання.
Координатний промінь - це промінь, який має початок в точці О (початок відліку) і одиничний відрізок.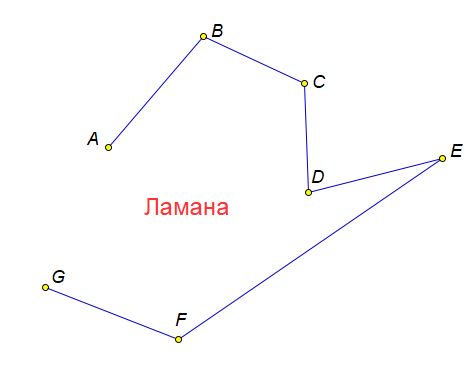
2) Два відрізки називаються рівними, якщо вони суміщаються при накладанні. Рівні відрізки мають рівні довжини.
3) Довжина відрізка - це відстань між точками, які зображують кінці відрізка.
4) Якщо відрізки розташувати послідовно один за одним, то отримаєте фігуру, яка називається ламана. Довжина ламаної дорівнює сумі довжин усіх її ланок.
--------------------------------------------------------------------------
4. КУТИ.
1) Фігуру, утворену двома променями , які мають спільний початок, називають кутом.
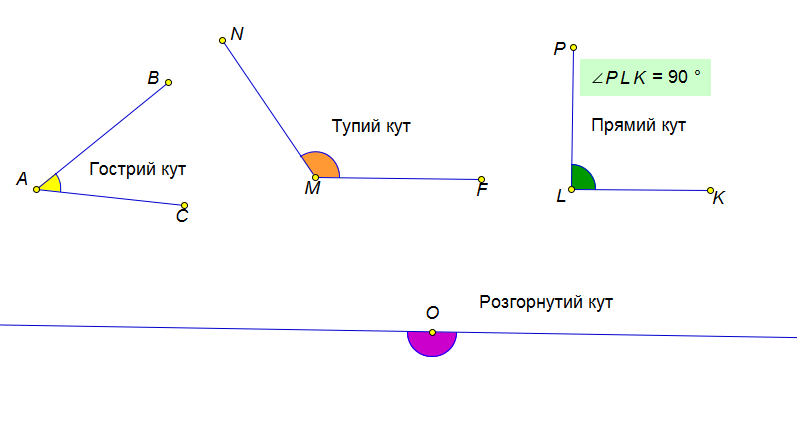
2) Види кутів: прямий (градусна міра якого = 900),
гострий (градусна міра якого менша за 900),
тупий (градусна міра якого більша за 900 , але менша за 1800),
розгорнутий (градусна міра якого = 1800).
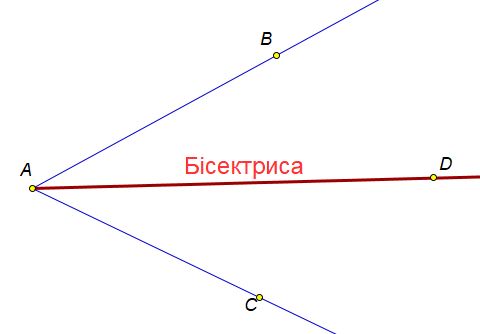
3) Бісектриса кута - промінь, який ділить кут на два рівних кути.
--------------------------------------------------------------------------
5. ТРИКУТНИКИ.
1) Види трикутників:
(відносно кутів) : гострокутні (всі кути гострі);
прямокутні (один кут прямий, тобто = 900)
тупокутні (один із кутів тупий)
(відносно сторін) : різносторонній (всі сторони різної довжини);
рівнобедрений (дві сторони однієї довжини);
правильний або рівносторонній (всі сторони однакової довжини).
2) Периметр трикутника Р = a + b + c (сума довжин всіх сторін)
--------------------------------------------------------------------------
6. ПРЯМОКУТНИК.
1) Чотирикутник, у якого всі кути прямі, називається прямокутником.
2) Протилежні сторони прямокутника рівні.
3) Периметр прямокутника: P = 2a + 2b або P = 2(a + b)
4) Площа прямокутника: S = a * b.
5) Прямокутник, у якого всі сторони рівні, називається квадрат.
6) Периметр квадрата: P = 4a
7) Площа квадрата: S = a2
--------------------------------------------------------------------------
7. Додавання і віднімання натуральних чисел.
1) На координатному промені з двох натуральних чисел більше число розташоване правіше від меншого.
2) Додавання.
Переставна властивість і сполучна властивість. Якщо один із доданків = нулю, то сума = другому доданку.
Щоб знайти невідомий доданок, треба від суми відняти відомий доданок
3) Віднімання.
Різниця a - b показує, на скільки число a більше від числа b.
Щоб знайти невідоме зменшуване, треба до різниці додати від'ємник.
Щоб знайти невідомий від'ємник, треба від зменшуваного відняти різницю.
4) Правило віднімання суми від числа:
Щоб від числа відняти суму двох доданків, можна від цього числа відняти один із доданків і потім від результату відняти другий доданок.
a - (b + c) = a - b - c = a - c - b
5) Правило віднімання числа від суми:
Щоб від суми двох доданків відняти число, можна відняти це число від одного з доданків (якщо цей доданок більший або дорівнює від'ємнику) і потім до результату додати другий доданок.
(a + b) - c = a - c + b = b - c + a
--------------------------------------------------------------------------
8. Формула шляху.
1) Рівність 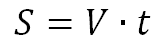 , де
, де
S - пройдений шлях у км (м, см, дм) ;
V - швидкість руху у км/год (м/с, м/хв);
t - час у год. (хв, с)
Щоб знайти невідомі елементи при руху об'єкта по річці, треба
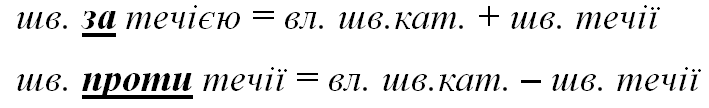
--------------------------------------------------------------------------
9. Множення і ділення.
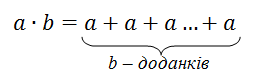
1) а * 1 = а; а * 0 = 0; 0 * 0 = 0;
0 : а = 0; а : а = 1; а : 1 = а;
на нуль ділити не можна!
2) Розподільна властивість множення:
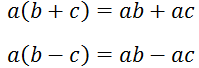
Таке перетворення ще називають розкриття дужок.
3) Щоб знайти невідомий множник, треба добуток поділити на відомий множник.
Щоб знайти невідоме ділене, треба частку помножити на дільник.
Щоб знайти невідомий дільник, треба ділене поділити на частку.
--------------------------------------------------------------------------
10. Степінь числа.
Степінь числа - це запис спеціальний одинакових множників.
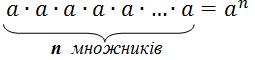
Наприклад, 7*7*7*7*7 = 75 і читають "сім у п'ятому степені".
Вираз 75 - називають степенем, де
7 - основа степеня;
5 - показник степеня, який показує, скільки разів множили основу.
Піднесення до степеня у виразі є дією першого ступеня.
--------------------------------------------------------------------------
11. Тіла у просторі.
1) Прямокутний паралелепіпед.
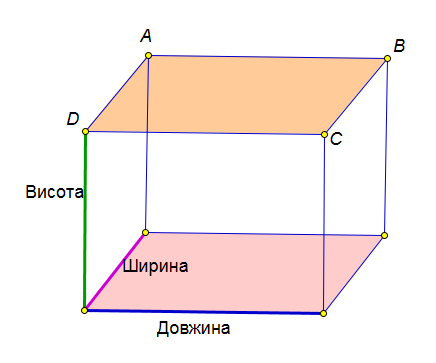
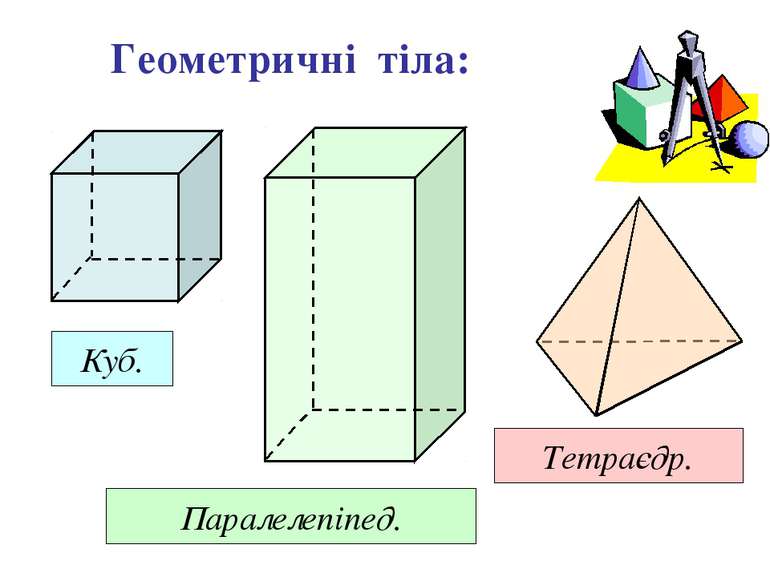

--------------------------------------------------------------------------
12. Звичайні дроби.
1) Якщо чисельник дробу = знаменнику, то такий дріб = 1;
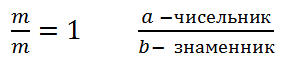
2) Правильний дріб - це дріб, у якого чисельник менший від знаменника.
3) Дріб, у якого чисельник менший від знаменника, називають правильним.
4) Із двох дробів із однаковими знаменниками більший той, у якого чисельник більший.
Із двох дробів з однаковими чисельниками більший той, у якого знаменник менший.
Усі правильні дроби менші від одиниці.
Кожний правильний дріб менший за будь-який неправильний.
5) Щоб знайти суму двох дробів з однаковими знаменниками, треба додати їх чисельники, а знаменник залишити той самий.
6) Мішане число - число, яке містить цілу та дробову частини. Дробова частина - завжди правильний дріб.
7) Щоб перетворити неправильний дріб у мішане число, треба чисельник поділити на знаменник. Частка при діленні - це ціла частина, остача - чисельник правильного дробу, знаменник - не змінюється.
8) Щоб перетворити мішане число у неправильний дріб, треба знаменник дробу помножити на цілу частину і додати чисельник. Отримане число - це є чисельник (над рискою) неправильного дробу. Знаменник не змінюється.
9) Щоб знайти суму двох мішаних чисел, треба окремо додати цілі і дробові частини.
--------------------------------------------------------------------------
13. Десяткові дроби.
1) Запис дробової частини десяткового дробу містить стільки цифр, скільки нулів у записі знаменника відповідного звичайного дробу.
2) При порівнянні десяткових дробів з різною кількістю знаків після коми, треба зрівняти кількість цифр у дробових частинах.
3) Округлення.
Підкреслити цифру розряду, до якого треба округлити.
Подивитись на цифру, яка стоїть після підкресленої.
Якщо ця цифра - 0, 1, 2, 3, 4 , - то підкреслену цифру залишаємо, а після неї інші цифри відкидаємо.
Якщо цифра - 5, 6, 7, 8, 9, - то підкреслену цифру збільшуємо на 1, а після неї інші цифри відкидаємо.
4) При додаванні та відніманні десяткових дробів кількість цифр після коми треба зрівняти (якщо в одному числі їх менше, то дописати нулі в кінці числа). Числа записують одне під одним так, щоб кожний розряд числа відповідав кожному розряду іншого числа.
5) Множення десяткових дробів виконують, як множення натуральних чисел, не звертаючи уваги на кому. У отриманому добутку від останньої цифри комою відокремлюють стільки цифр, скільки їх разом у двох множниках.
6) Ділення десяткового дробу на натуральне число. Спочатку виконується ділення цілої частини, потім ставиться кома у частку і продувжуєте виконувати ділення далі.
7) Ділення на десятковий дріб. Треба перенести коми у діленому і дільнику на стільки цифр, скільки їх є після коми у дільнику. Далі виконати ділення на натуральне число.
8) Щоб помножити десятковий дріб на 0,1 ; 0,01 ; 0,001 і т.д., треба перенести кому вліво на 1; 2; 3 цифри відповідно.
Щоб помножити десятковий дріб на 10 ; 100 ; 1000 і т.д., треба перенести кому вправо на 1; 2; 3 цифри відповідно.
Щоб поділити десятковий дріб на 0,1 ; 0,01 ; 0,001 і т.д., треба перенести кому вправо на 1; 2; 3 цифри відповідно.
Щоб поділити десятковий дріб на 10 ; 100; 1000 і т.д., треба перенести кому вліво на 1; 2; 3 цифри відповідно.
9) Якщо ділене і дільник одночасно збільшити одночасно у 10; 100; 1000 і т.д. разів, то частка не зміниться.
---------------------------------------------------------------------------
14. Середнє арифметичне.
1) Середнє арифметичне кількох чисел - це частка від ділення суми всіх цих чисел на їх кількість.
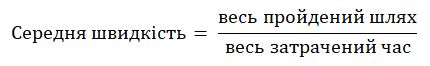
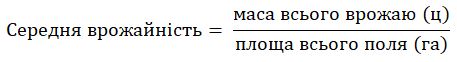

---------------------------------------------------------------------------
15. Відсотки.
1) Відсоток (процент) - це одна сота частина числа.
2) Щоб знайти відсоток від числа, треба це число помножити на відсоток, записаний у вигляді десяткового дробу.



